Estimate sums and differences of mixed numbers
key notes:
1. Understanding Mixed Numbers
- A mixed number is a number that consists of an integer (whole number) and a proper fraction. For example, 3 1/2, 5 3/4, etc.
- Example: 4 2/5 means 4 whole parts and 2/5 of another part.
2. Estimation of Sums and Differences
- Estimating sums and differences involves rounding the mixed numbers to simpler numbers (often whole numbers or fractions that are easier to work with) to quickly calculate an approximate answer.
3. Rounding Mixed Numbers
- Round the whole number to the nearest whole number if necessary.
- Round the fraction to a simpler fraction, typically 1/2, 1/4, or 1, depending on the fraction.
- If the fraction is 1/8 or smaller, round it down to 0.
- If the fraction is 3/8 or greater, round it up to 1/2.
4. Estimating Sums
- When adding mixed numbers, round each mixed number to a convenient whole number or simple fraction.
- Example: Estimate the sum of 3 2/3 and 5 3/8:
- Round 3 2/3 to 4 and 5 3/8 to 5.
- Estimate sum: 4 + 5 = 9.
5. Estimating Differences
- For subtraction, round each mixed number to a simpler form.
- Example: Estimate the difference between 6 5/8 and 3 1/4:
- Round 6 5/8 to 7 and 3 1/4 to 3.
- Estimate difference: 7 – 3 = 4.
6. Steps for Estimating Sums and Differences
- Step 1: Round the mixed numbers to whole numbers or simple fractions.
- Step 2: Add or subtract the whole numbers and fractions.
- Step 3: Check if the estimation makes sense by comparing it to the exact calculation.
Learn with an example
Estimate the sum.
Round each number to the nearest whole number, then add.
14 1/3 + 3 5/18
The sum is approximately __________.
Round each number to the nearest whole number.

Estimate the difference.
Round each number to the nearest whole number, then subtract.
10 3/8 – 8 7/10
The difference is approximately_________.
Round each number to the nearest whole number.
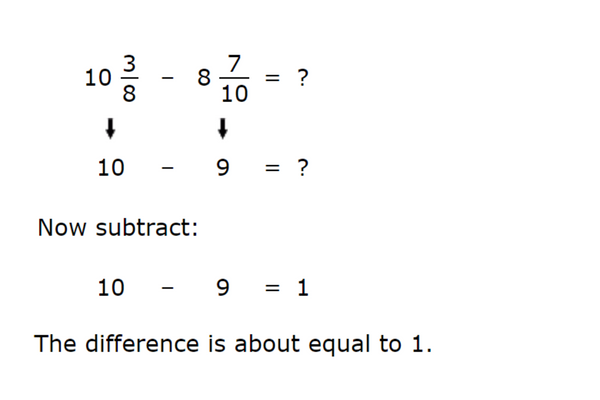
Estimate the sum.
Round each number to the nearest whole number, then add.
5 1/18 + 4 1/15
The sum is approximately ____ .
Round each number to the nearest whole number.

Now add:
5 + 4 = 9
The sum is about equal to 9.
let’s practice:

