Compare fractions with like and unlike denominators

key notes:

1. Fractions with Like Denominators:

  • Fractions with the same denominator are easier to compare because the denominator represents the total number of equal parts.
  • How to compare:
    • Compare the numerators directly (the bigger numerator represents the bigger fraction).
    • Example: Compare 3/7​ and 5/7​. Since both fractions have the same denominator, 5/7 is greater because 5 is larger than 3.

2. Fractions with Unlike Denominators:

  • When the fractions have different denominators, you cannot directly compare them. You need to make the denominators the same.
  • How to compare:
    1. Find a common denominator: This is usually the least common denominator (LCD), which is the smallest multiple that both denominators share.
    2. Rewrite the fractions: Multiply the numerator and denominator of each fraction by a number that makes the denominators the same.
    3. Compare the numerators: Once the fractions have like denominators, compare the numerators.
  • Example: Compare 2/5​ and 3/8​:
    • The least common denominator of 5 and 8 is 40.

3. Simplifying Fractions:

  • Before comparing fractions, simplify them if necessary to make the comparison easier.

4. Using Visual Models:

  • You can also use visual models, such as fraction bars or circles, to help compare fractions. This is particularly useful for understanding why fractions with the same denominator are easier to compare.

5. Fraction Comparison Symbols:

  • Use the symbols < (less than), > (greater than), or = (equal to) to express the relationship between fractions after comparing them.

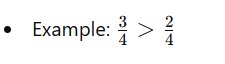
Learn with an example

Which fraction is greater?

A} 1/10

B} 8/10

You can use models to compare fractions.

1 out of 10 equal parts is colored.

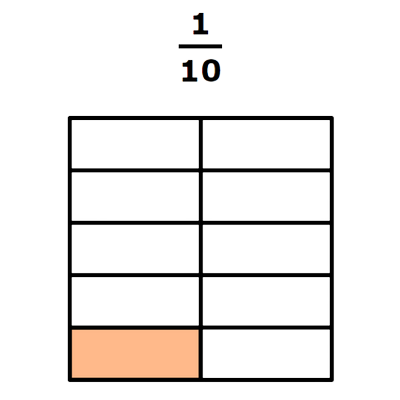
8/10

8 out of 10 equal parts are colored.

Both shapes have 10 equal parts and are the same size. So, the parts in the first shape are the same size as the parts in the second shape.

When parts are the same size, 8 parts is more than 1 part. So, more of the second shape is colored.

8/10 is greater than 1/10.

Which fraction is less?

A} 1/4

B} 3/4

You can use models to compare fractions.

1/4

1 out of 4 equal parts is colored.

3/4

3 out of 4 equal parts are colored.

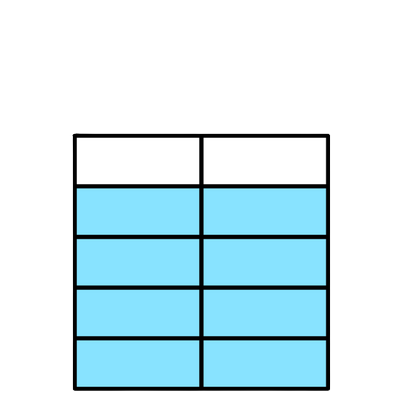
Both shapes have 4 equal parts and are the same size. So, the parts in the first shape are the same size as the parts in the second shape.

When parts are the same size, 1 part is less than 3 parts. So, less of the first shape is colored.

1/4 is less than 3/4.

Which fraction is less?

A} 1/2

B} 1/12

You can use models to compare fractions.

1/2

1 out of 2 equal parts is colored.

1/12

1 out of 12 equal parts is colored.

Both shapes have 1 colored part, but the part in the second shape is smaller. This is because the second shape is sliced into 12 parts, instead of 2.

So, less of the second shape is colored.

1/12 is less than 1/2.

Let’s practice!