Inequalities with decimals
key notes:
| What are Inequalities? |
Inequalities are mathematical statements that compare two expressions using symbols such as:
>(greater than)<(less than)≥(greater than or equal to)≤(less than or equal to)≠(not equal to)
| Decimal Numbers in Inequalities: |
Decimals are numbers that contain a decimal point (e.g., 3.5, 0.75, 2.13).
Decimals can be compared using inequality symbols just like whole numbers.
| Steps to Compare Decimals: |
Step 1: Align the decimal points.
Step 2: Compare the digits from left to right.
Step 3: If the digits are the same, move to the next place value (tenths, hundredths, thousandths, etc.) until you find a difference.
Example: 3.45 > 3.4 (because 3.45 has a 5 in the hundredths place, while 3.4 has 0).
| Example Inequalities with Decimals: |
Example 1: 5.3 > 4.8
Example 2: 2.5 ≤ 2.5
Example 3: 0.75 ≠ 1.25
| Solving Inequalities with Decimals: |
Just like whole number inequalities, you can solve inequalities with decimals by applying the same rules:
- Add, subtract, multiply, or divide both sides of the inequality by the same number.
- When multiplying or dividing by a negative number, flip the inequality sign.
Example: 1.2 + 0.3 < 2.0 (simplify to 1.5 < 2.0).
Which number is bigger, 8.019 or 8.03?
Follow the steps:
- Write the numbers with the decimal points lined up.
| 8 | . | 0 | 1 | 9 |
| 8 | . | 0 | 3 |
- Starting at the far left, which is the largest place value, compare the numbers.
The digit in the ones place in both numbers is an 8.
- If the first place value is the same in both numbers, move one spot to the right and compare again.
The digit in the tenths place in both numbers is a 0.
- If the second place value is the same in both numbers, move one spot to the right and compare again.
The digit in the hundredths place in the top number is a 1, and it is a 3 in the bottom number.
- The number with the larger digit is the larger number.
Since 3 is bigger than 1, then 8.03 > 8.019
8.03 > 8.019
Learn with an example
Which sign makes the statement true?
0.011? 0.811
- >
- <
Use a place value chart. Be sure to line up the decimal points.
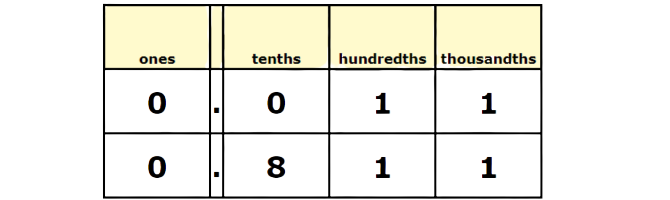
Compare the digits, starting with the highest place value. The ones digits are the same. The tenths digits are different. The tenths digit in 0.011 is less than the tenths digit in 0.811.
0.011 is less than 0.811.
Use the less-than sign.
0.011 < 0.811
Which sign makes the statement true?
0.68 ? 0.63
- >
- <
Use a place value chart. Be sure to line up the decimal points.
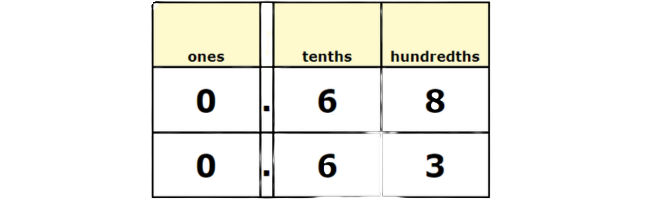
Compare the digits, starting with the highest place value. The ones and tenths digits are the same. The hundredths digits are different. The hundredths digit in 0.68 is greater than the hundredths digit in 0.63.
0.68 is greater than 0.63.
Use the greater-than sign.
0.68 > 0.63
Which sign makes the statement true?
0.5 ? 0.7
- >
- <
Use a place value chart. Be sure to line up the decimal points.
| ones | tenths | |
| 0 | . | 5 |
| 0 | . | 7 |
Compare the digits, starting with the highest place value. The ones digits are the same. The tenths digits are different. The tenths digit in 0.5 is less than the tenths digit in 0.7.
0.5 is less than 0.7.
Use the less-than sign.
0.5 < 0.7

let’s practice:

