Highest common factor
key notes:
| What is HCF? |
The full form of HCF is Highest Common Factor. HCF of two numbers is the highest factor that can divide the two numbers, evenly. HCF can be evaluated for two or more than two numbers. It is the greatest divisor for any two or more numbers, that can equally or completely divide the given numbers.
For Example: The Highest common factor of 60 and 75 is 15 because 15 is the largest number which can divide both 60 and 75 exactly.
| How to Find HCF? |
We can find the HCF of any given numbers by using two methods:
- by prime factorization method
- by division method
Let us discuss these two methods one by one in this article.
| HCF By Prime Factorization Method |
Follow the below-given steps to find the HCF of numbers using the prime factorisation method.
- Step 1: Write each number as a product of its prime factors. This method is called here prime factorization.
- Step 2: Now list the common factors of both the numbers
- Step 3: The product of all common prime factors is the HCF ( use the lower power of each common factor)
Example 1: Evaluate the HCF of 60 and 75.
Solution:

Example 2: Find the HCF of 36, 24 and 12.
Solution:

| HCF By Division Method |
You have understood by now the method of finding the highest common factor using prime factorization. Now let us learn here to find HCF using the division method. Basically, the division method is nothing but dividing the given numbers, simultaneously, to get the common factors between them. Follow the steps mentioned below to solve the problems of HCF.
- Step 1: Write the given numbers horizontally, in a sequence, by separating them with commas.
- Step 2: Find the smallest prime number which can divide the given number. It should exactly divide the given numbers. (Write on the left side).
- Step 3: Now write the quotients.
- Step 4: Repeat the process, until you reach the stage, where there is no coprime number left.
- Step 5: We will get the common prime factors as the factors on the left-hand side divides all the numbers exactly. The product of these common prime factors is the HCF of the given numbers.
Let us understand the above-mentioned steps to find the HCF by division method with the help of examples.
Problem 1: Evaluate the HCF of 30 and 75
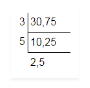
As we can note that the mentioned prime factors, on the left side, divide all the numbers exactly. So, they all are common prime factors. We have no common prime factor for the numbers remaining at the bottom.
So, HCF = 3 × 5 = 15.
Problem 2: Find out HCF of 36, and 24
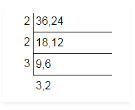
HCF = 2 × 2 × 3 = 12.
| HCF by Shortcut method |
Steps to find the HCF of any given set of numbers.
- Step 1: Divide the larger number by the smaller number first, such as;
Larger Number/Smaller Number
- Step 2: Divide the divisor of step 1 by the remainder left.
Divisor of step 1/Remainder
- Step 3: Again divide the divisor of step 2 by the remainder.
Divisor of step 2/Remainder
- Step 4: Repeat the process until the remainder is zero.
- Step 5: The divisor of the last step is the HCF.
| How to find the HCF of Three numbers |
| 1) Calculate the HCF of 2 numbers. |
| 2) Then Find the HCF of the 3rd number and the HCF found in step 1. |
| 3) The HCF you got in step 2 will be the HCF of the 3 numbers. |
Learn with an example
🔔 What is the highest common factor of 8 and 16?
List the factors of each number. Find the largest number that appears in both lists.
Factors of 8: 8, 4, 2, 1
Factors of 16: 16, 8, 4, 2, 1
The highest common factor of 8 and 16 is 8.
🔔 What is the highest common factor of 12 and 3?
List the factors of each number. Find the largest number that appears in both lists.
Factors of 12: 12, 6, 4, 3, 2, 1
Factors of 3: 3, 1
The highest common factor of 12 and 3 is 3.
🔔 What is the highest common factor of 9 and 18?
List the factors of each number. Find the largest number that appears in both lists.
Factors of 9: 9, 3, 1
Factors of 18: 18, 9, 6, 3, 2, 1
The highest common factor of 9 and 18 is 9.
Let’s practice!🖊️

