Prime factorization

key notes:

What is Prime Factorization?

Prime factorization is defined as a way of finding the prime factors of a number, such that the original number is evenly divisible by these factors. As we know, a composite number has more than two factors, therefore, this method is applicable only for composite numbers and not for prime numbers.

For example, the prime factors of 126 will be 2, 3 and 7 as 2 × 3 × 3 × 7 = 126 and 2, 3, 7 are prime numbers.

Prime factorization Examples

• Prime factorization of 12 is 2 × 2 × 3 = 2² × 3
• Prime factorization of 18 is 2 × 3 × 3 = 2 × 3²
• Prime factorization of 24 is 2 × 2 × 2 × 3 = 2³ × 3
• Prime factorization of 20 is 2 × 2 × 5 = 2² × 5
• Prime factorization of 36 is 2 × 2 × 3 × 3 = 2² × 3²

Prime Factors of a Number :

Prime factors of a number are the set of prime numbers which when multiplied by together give the actual number. Also, we can say, the prime factors divide the number completely. It is similar to factoring a number and considering only the prime numbers among the factors. For example, the prime factors of 6 will be 2 and 3, the prime factors of 26 will be 13 and 2, etc.

Prime Factorization Methods

The most commonly used prime factorization methods are:

• Division Method
• Factor Tree Method

Division Method

The steps to calculate the prime factors of a number is similar to the process of finding the factors of a large number. Follow the below steps to find the prime factors of a number using the division method:

• Step 1: Divide the given number by the smallest prime number. In this case, the smallest prime number should divide the number exactly.
• Step 2: Again, divide the quotient by the smallest prime number.
• Step 3: Repeat the process, until the quotient becomes 1.
• Step 4: Finally, multiply all the prime factors

Factor Tree Method

To find the prime factorization of the given number using factor tree method, follow the below steps:

• Step 1: Consider the given number as the root of the tree
• Step 2: Write down the pair of factors as the branches of a tree
• Step 3: Again factorize the composite factors, and write down the factors pairs as the branches
• Step 4: Repeat the step, until to find the prime factors of all the composite factors

In factor tree, the factors of a number are found and then those numbers are further factorized until we reach the closure. Suppose we have to find the factors of 60 and 282 using a factor tree. Then see the diagram given below to understand the concept.

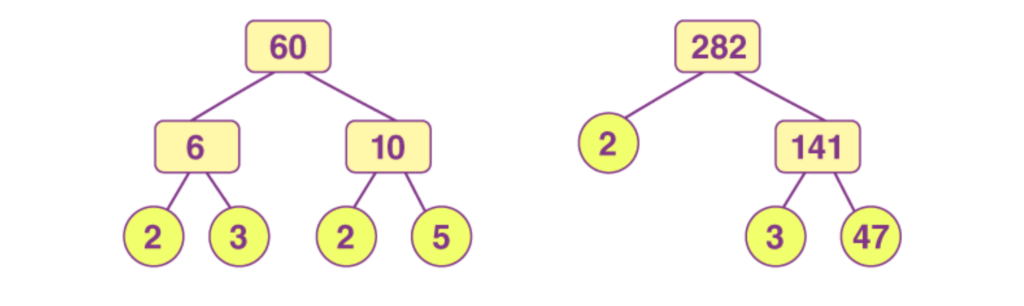
In the above figure, we can number 60 is first factorized into two numbers i.e. 6 and 10. Again, 6 and 10 is factorized to get the prime factors of 6 and 10, such that;

6 = 2 x 3

and 10 = 2 x 5

If we write the prime factors of 60 altogether, then;

Prime factorization of 60 = 6 x 10 = 2 x 3 x 2 x 5

Same is the case for number 282, such as;

282 = 2 x 141 = 2 x 3 x 47

So in both cases, a tree structure is formed

Prime Factorization Solved Examples

An example question is given below which will help to understand the process of calculating the prime factors of a number easily.

Q.1: Find the prime factors of 1240.

∴ The Prime Factors of 1240 will be 2³ × 5 × 31.

Q.2: Find the prime factors of 544.

Therefore, the prime factors of 544 are 2⁵ x 17.

Learn with an example

Let’s practice!🖊️