Identify factors
key notes:
| Definition of Factors: |
- A factor of a number is a whole number that can be multiplied by another whole number to get the original number.
- Example: Factors of 12 include 1, 2, 3, 4, 6, and 12 because 1×12=12 , 2×6=12, and 3×4=12.

| Understanding Factors: |
- Factors are always less than or equal to the number.
- Every number has at least two factors: 1 and the number itself.
| Finding Factors: |
- Step 1: Start with 1 and the number itself.
- Step 2: Divide the number by each integer starting from 2 up to the square root of the number.
- Step 3: If the division results in a whole number (no remainder), both the divisor and the quotient are factors.
- Example: To find the factors of 18, divide 18 by 1, 2, 3, 6, 9, and 18. The factors of 18 are 1, 2, 3, 6, 9, and 18.
| Prime Factorization: |
Prime factorization is a process of factoring a number in terms of prime numbers i.e. the factors will be prime numbers. Here, all the concepts of prime factors and prime factorization methods have been explained which will help the students understand how to find the prime factors of a number easily.
For example, the prime factors of 126 will be 2, 3 and 7 as 2 × 3 × 3 × 7 = 126 and 2, 3, 7 are prime numbers.
| Prime factorization Examples |
- Prime factorization of 12 is 2 × 2 × 3 = 22 × 3
- Prime factorization of 18 is 2 × 3 × 3 = 2 × 32
- Prime factorization of 24 is 2 × 2 × 2 × 3 = 23 × 3
- Prime factorization of 20 is 2 × 2 × 5 = 22 × 5
- Prime factorization of 36 is 2 × 2 × 3 × 3 = 2² × 3²
| Factor Pairs: |
- Factors come in pairs that multiply to give the original number.
- Example: The factor pairs of 18 are (1, 18), (2, 9), and (3, 6).
| Common Factors: |
- When two numbers share factors, those shared numbers are called common factors.
- Example: Common factors of 12 and 18 are 1, 2, 3, and 6.
| Greatest Common Factor (GCF): |
The largest number, which is the factor of two or more number is called the Greatest Common Factor (GCF). It is the largest number (factor) that divide them resulting in a Natural number.
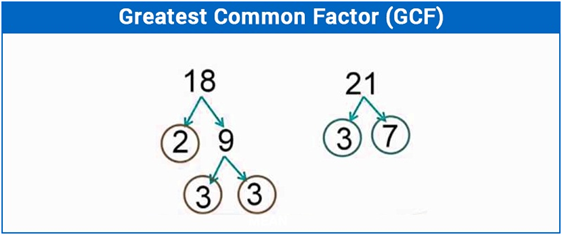
| Examples for Practice: |
Example 1: Find the factors of 24.
- Start with 1 and 24. Then, check 2, 3, 4, 6, 8, and 12.
- Factors: 1, 2, 3, 4, 6, 8, 12, 24.
Example 2: Find the common factors of 30 and 45.
- Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
- Factors of 45: 1, 3, 5, 9, 15, 45.
- Common factors: 1, 3, 5, 15.
Example 3: Identify the greatest common factor of 28 and 42.
- Factors of 28: 1, 2, 4, 7, 14, 28.
- Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42.
- GCF: 14.
Learn with an example
1,2,4,8,16 are the factors of 16.
Which numbers are factors of 15?
1 / 3 / 5 / 15
divide all the numbers into 15, and see which ones divide evenly.
| 15 ÷ 5 = 3 R0 | Yes, 5 divides evenly | |
| 15 ÷ 15 = 1 R0 | Yes, 15 divides evenly | |
| 15 ÷ 3 = 5 R0 | Yes, 3 divides evenly | |
| 15 ÷ 1 = 15 R0 | Yes, 1 divides evenly |
1, 5, 3, and 15 divide evenly into 15, so 1, 5, 3, and 15 are factors.
Which number is a factor of 9?
2 / 4 / 3 / 8
Divide all the numbers into 9, and see which one divides evenly.
| 9 ÷ 2 = 4 R1 | No | |
| 9 ÷ 4 = 2 R1 | No | |
| 9 ÷ 3 = 3 R0 | Yes, 3 divides evenly | |
| 9 ÷ 8 = 1 R1 | No |
3 divides evenly into 9, so 3 is a factor.
Which numbers are factors of 12?
Select all that apply.
- 12
- 9
- 7
- 2
Divide all the numbers into 12, and see which ones divide evenly.
| 12 ÷ 12 = 1 R0 | Yes, 12 divides evenly | |
| 12 ÷ 9 = 1 R3 | No | |
| 12 ÷ 7 = 1 R5 | No | |
| 12 ÷ 2 = 6 R0 | Yes, 2 divides evenly |
2 and 12 divide evenly into 12, so 2 and 12 are factors.
Let’s practice!🖊️

