Prime or composite
key notes:
| Prime Numbers: |
Definition: A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Examples: 2, 3, 5, 7, 11, 13, 17, etc.
Characteristics:
- Prime numbers have exactly two distinct positive divisors: 1 and the number itself.
- They cannot be formed by multiplying two smaller natural numbers.
- The number 2 is the only even prime number.

| 🧨Composite Numbers: |
Definition: A composite number is a natural number greater than 1 that has more than two positive divisors.
Examples: 4, 6, 8, 9, 10, 12, 14, etc.
Characteristics:
Composite numbers have more than two distinct positive divisors.
They can be formed by multiplying two or more smaller natural numbers.
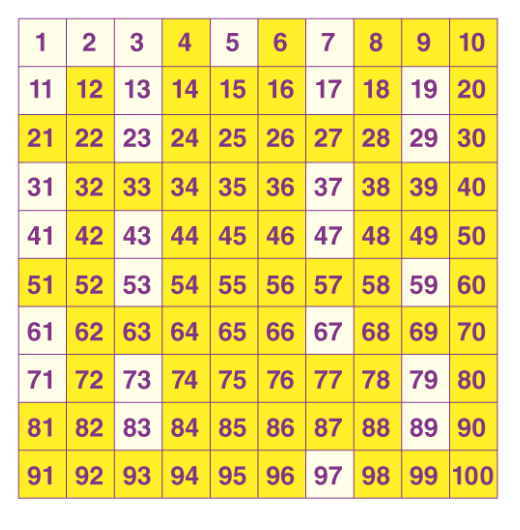
| 🧨Identifying Prime and Composite Numbers: |
| prime numbers: |
How to Find Prime Numbers?
The following two methods will help you to find whether the given number is a prime or not.
Method 1:
We know that 2 is the only even prime number. And only two consecutive natural numbers which are prime are 2 and 3. Apart from those, every prime number can be written in the form of 6n + 1 or 6n – 1 (except the multiples of prime numbers, i.e. 2, 3, 5, 7, 11), where n is a natural number.
For example:
6(1) – 1 = 5
6(1) + 1 = 7
6(2) – 1 = 11
6(2) + 1 = 13
6(3) – 1 = 17
6(3) + 1 = 19
6(4) – 1 = 23
6(4) + 1 = 25 (multiple of 5)
…
Method 2:
To know the prime numbers greater than 40, the below formula can be used.
n2 + n + 41, where n = 0, 1, 2, ….., 39
For example:
(0)2 + 0 + 0 = 41
(1)2 + 1 + 41 = 43
(2)2 + 2 + 41 = 47
| Composite numbers : |
How to Find the Composite Number?
The procedures to find whether a given number is prime or composite:
- Find all the factors of the positive integer
- A number is said to be prime if it has only two factors, 1 and itself
- If the number has more than two factors, then it is a composite
| Example: Find if 14 is a composite number. Let us find the factors of 14. 14÷1 = 14 14÷2 = 7 14÷7 = 2 14÷14 = 1 As we can see, the factors of 14 are 1,2,7 and 14, so it is a composite number. |
Learn with an example
🔔 Which number is prime?
- 2
- 6
- 14
- 1
The factors of 2 are 1 and 2. Since the only factors of 2 are 1 and itself, 2 is prime.
The factors of 6 are 1, 2, 3, and 6. Since 6 has more factors than just 1 and itself, 6 is not prime.
The factors of 14 are 1, 2, 7, and 14. Since 14 has more factors than just 1 and itself, 14 is not prime.
The only factor of 1 is 1. 1 is special because it is neither prime nor composite. So, 1 is not prime.
The prime number is 2.
🔔 Which number is prime?
- 14
- 8
- 9
- 17
- The factors of 14 are 1, 2, 7, and 14. Since 14 has more factors than just 1 and itself, 14 is not prime.
- The factors of 8 are 1, 2, 4, and 8. Since 8 has more factors than just 1 and itself, 8 is not prime.
- The factors of 9 are 1, 3, and 9. Since 9 has more factors than just 1 and itself, 9 is not prime.
- The factors of 17 are 1 and 17. Since the only factors of 17 are 1 and itself, 17 is prime.
- The prime number is 17.
Select all the numbers that are prime.
- 19
- 3
- 7
- 11
- The factors of 19 are 1 and 19. Since the only factors of 19 are 1 and itself, 19 is prime.
- The factors of 3 are 1 and 3. Since the only factors of 3 are 1 and itself, 3 is prime.
- The factors of 7 are 1 and 7. Since the only factors of 7 are 1 and itself, 7 is prime.
- The factors of 11 are 1 and 11. Since the only factors of 11 are 1 and itself, 11 is prime.
- The prime numbers are 19, 3, 7, and 11.
Let’s practice!🖊️

