Multiply whole numbers
Key notes :
| Understanding Multiplication |
Definition: Multiplication is the process of adding a number to itself a certain number of times. Multiplication is a math operation used to find the total when you have equal groups.
It is a repeated addition.
➤ Example: 4 × 3 means 4 added 3 times → 4 + 4 + 4 = 12
Terminology:
- Multiplicand: The number being multiplied.
- Multiplier: The number by which the multiplicand is multiplied.
- Product: The result of the multiplication.
| Basic Properties of Multiplication |
Commutative Property: The order of factors does not change the product.
- Example: 3×4=4×3
Associative Property: The grouping of factors does not change the product.
- Example: (2×3)×4=2×(3×4)
Distributive Property: Multiplying a number by a sum is the same as doing each multiplication separately.
Identity Property: Any number multiplied by 1 remains the same.
- Example: 5×1=5
Zero Property: Any number multiplied by 0 is 0.
- Example: 6×0=0
| Multiplication Techniques |
Times Tables: Memorizing multiplication tables helps in quick calculation.
Repeated Addition: Understanding that multiplication is repeated addition.
- Example: 4×3=4+4+4=12
Skip Counting: Counting by numbers other than 1 to find the product.
- Example: Skip counting by 5s to find 5×4 : 5, 10, 15, 20.
Area Model: Breaking numbers into parts, multiplying each part, and then adding them.
- Example: To multiply 23 by 5, break 23 into 20 and 3: (20×5)+(3×5)=100+15=115 (20 \times 5) + (3 \times 5) = 100 + 15 = 115(20×5)+(3×5)=100+15=115.
| Simple Multiplication Techniques for Large Numbers |
Multiplying Large Numbers (2-digit × 2-digit)
Example: 34 × 12
34
×12
_______
68 ← 34 × 2 (ones place)
+ 340 ← 34 × 1 (tens place; shift one place to left)
_______
408
Answer: 408
| Break Down the Numbers (Distributive Property) |
Splitting Numbers into Parts: Break large numbers into smaller, more manageable parts, multiply each part separately, and then add the results
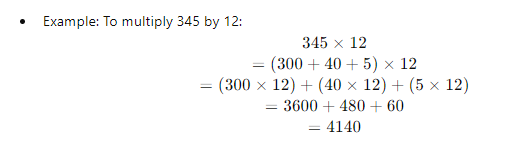
| Area Model (Box Method) |
| Column Method (Standard Algorithm) |
The Column Method, also known as the Standard Algorithm, is a step-by-step method of multiplying multi-digit numbers, writing each part in columns and adding partial products.
🧮 Steps to Use the Column Method
Let’s multiply: 326 × 4
326
×4
_______
1304
- Step-by-Step Multiplication: Write the numbers in columns, multiply each digit, starting from the rightmost digit, and add the partial products.
✅ Steps:
- Multiply 4 × 6 = 24 → Write 4, carry 2
- Multiply 4 × 2 = 8 → Add carry 2 → 8 + 2 = 10, write 0, carry 1
- Multiply 4 × 3 = 12 → Add carry 1 → 12 + 1 = 13
- Final answer: 1304
| 4. Lattice Method |
- Drawing a Grid: Draw a grid, split numbers into their individual digits, and multiply each digit, writing the results in the corresponding grid squares. Add the results along the diagonals.
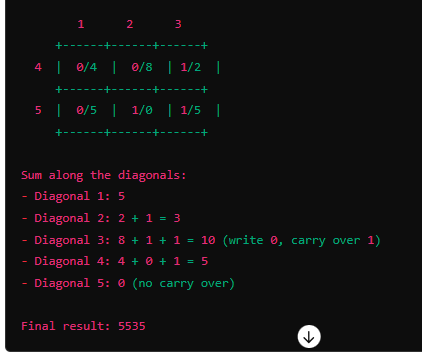
| 5. Estimation |
- Approximate and Adjust: Round the numbers to the nearest ten or hundred, perform the multiplication, and then adjust for the difference.
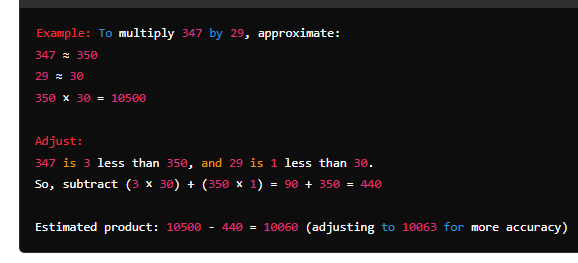
| Using Technology |
- Calculators: For very large numbers, use a calculator to ensure accuracy and save time.

- Spreadsheets: Use software like Excel or Google Sheets to handle large number multiplications easily.

| Practice Problems |
Solve the following:
- 124 × 3 = ___
- 205 × 12 = ___
- 92 × 100 = ___
- 18 boxes with 48 pens each. How many pens in total?
- Multiply using distributive property:
→ 7 × (20 + 3)
By applying these techniques, we can handle large number multiplications more efficiently and accurately.
| Real-Life Application (Word Problem) |
- Visual Representation: Use a box to break down the numbers into tens, hundreds, etc., and multiply each part separately.
Q: A box contains 24 pencils. How many pencils are in 15 boxes?
A: 24 × 15 = 360 pencils
Learn with an example
🗼 Multiply.
4 x 6172 =
- To make the problem easier, put the number with fewer digits on the bottom.
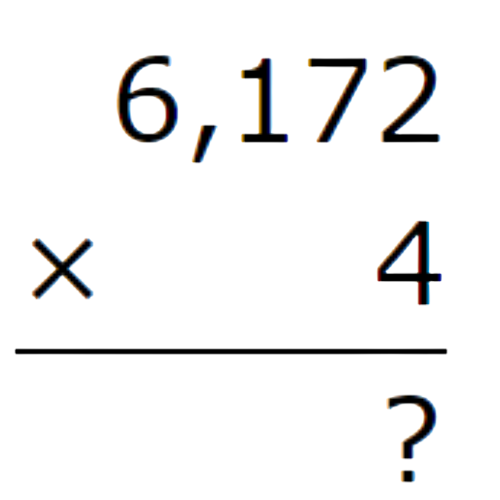
- Multiply the ones.
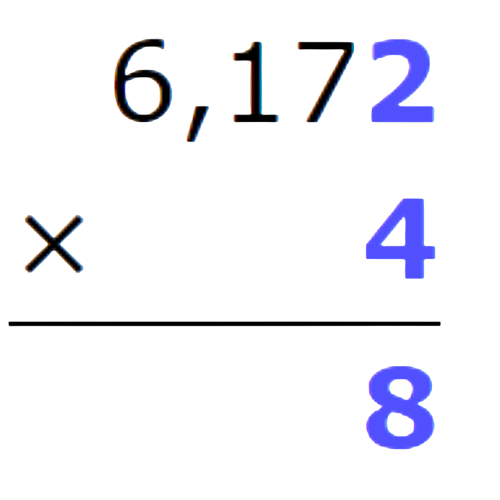
- Multiply the tens. Remember to carry over.
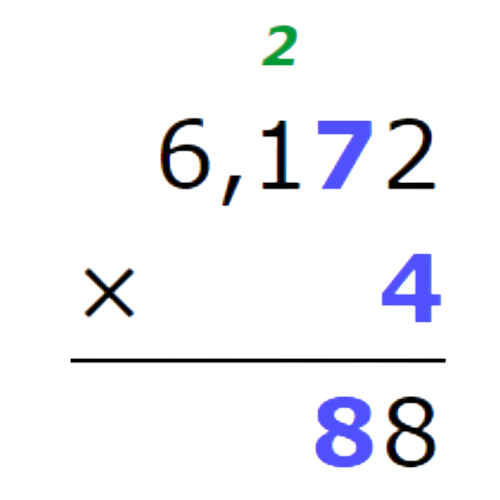
- Multiply the hundreds. Multiply 1 times 4, then add 2.
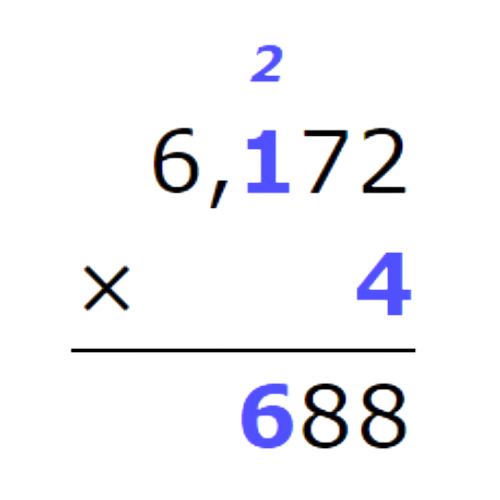
- Multiply the thousands.
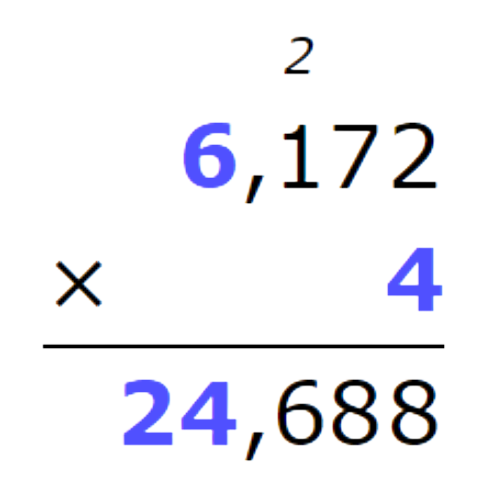
- The product is 24,688.
🗼 Multiply.
2×49 =
- To make the problem easier, put the number with fewer digits on the bottom.
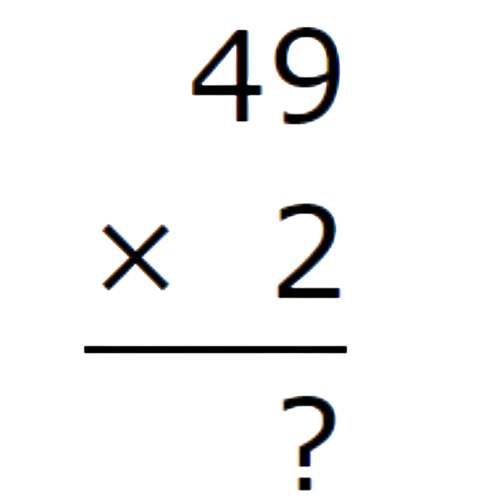
- Multiply the ones. Remember to carry over.
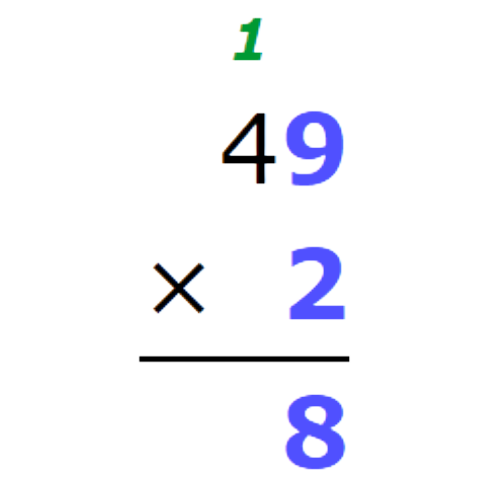
- Multiply the tens. Multiply 4 times 2, then add 1.
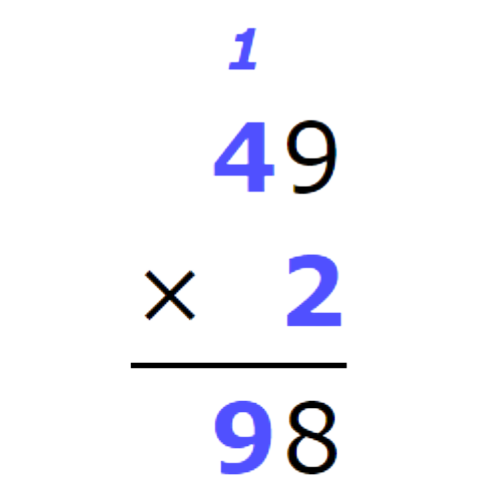
- The product is 98.
Let’s practice!🖊️

